Modular arithmetic

Modulus: q > 2
a=b (mod q ) means that a–b is an integer multiple of q.
r=a mod q means that r is the remainder upon dividing the integer a by q (so 0 ≤ r ≤ q-1).
Integers modulo q: \(Z_q = {0,1,2,..., q - 1}\), where addition, subtraction and multiplication are performed modulo q.
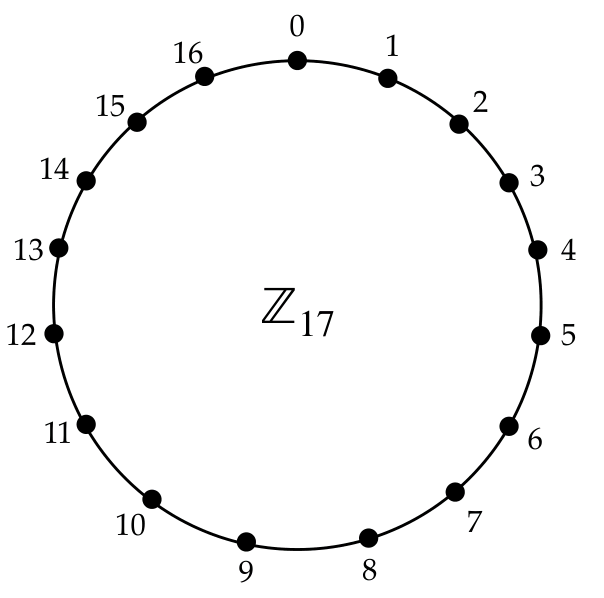
Example: \(Z_{17} = {0,1,2,3,4,5,6,7,8,9,10,1 1,12, 13, 14, 15, 16}\).
- In \(Z_{17}\), 9+ 15 =7, 9-15 = 11, and 9x 15 = 16.
- More precisely, 9 + 15 = 24 =7 (mod 17), 9-15 = -6 =11 (mod 17), and 9 x 15 = 135 = 16 (mod 17).

Polynomial rings

Let q be a prime modulus.
\(Z_q[x]\) is the set of all polynomials in x with coefficients in \(Z_q\)
When adding, subtracting, multiplying and dividing polynomials in \(Z_q[x]\), all coefficient arithmetic is performed in \(Z_q\)
Example: Let q =7, and consider \(f(x) = 5 + 4x^2+ 3x^3\) ∈ \(Z_7[x]\) and \(g(x) =6+ 3x + 2x^2\) ∈ \(Z_7[x]\). Then:
- \(f(x)+g(x)= 4+3x + 6x^2+3x^3\).
- \(f(x)-g(x) = 6+ 4x + 2x^2 +3x^3\).
- \[f(x)*g(x) = 2 +x+6x^2+ 2x^3 + 3x^4+6x^5\]

The polynomial ring \(R_q = ℤ_q[x]/(x^n + 1)\)

✦ Let q be a prime modulus, and let n be a positive integer. ✦ The polynomial ring \(R_q = ℤ_q[x]/(x^n + 1)\) is comprised of the polynomials in of \(ℤ_q[x]\) degree less than n , with multiplication of polynomials performed modulo the reduction polynomial \(x^n+1\).

✦ So, to multiply polynomials f(x),g(x) ∈ \(R_q\):

i. Multiply \(f(x)\) and \(g(x)\) in \(ℤ_q[x]\) obtaining a polynomial \(h(x)\) of degree at most 2n-2.
ii. Divide \(h(x)\) by \(x^n + 1\)to get a remainder polynomial of degree at most n-1.
iii. Then \(f(x)×g(x) = r(x)\) in \(R_q\)

✦ Note: The size of \(R_q\) is \(q^n\)

Example: The polynomial ring \(R_q = ℤ_{41}[x]/(x^4 + 1)\)

Let \(q = 41\) and \(n = 4\) .

✦ Then \(R_q\) is comprised of the polynomials in \(ℤ_{41}[x]\) of degree at most 3.

✦ Let \(f(x) = 32 + 17x^2 + 22x^3 ∈ R_q\) and \(g(x) = 11 + 7x + 19x^2 + x^3 ∈ R_q\) .

✦ In \(ℤ_{q}[x]\), \(h(x) = f(x) × g(x) = 24 + 19x + 16x^2 + 24x^3 + 26x^4 + 25x^5 + 22x^6\)

✦ The division of \(h(x)\) by \(x^4+1\) can be accomplished by replacing \(x^4\) by \(-1\) , \(x^5\) by \(-x\), and \(x^6\) by \(-x^2\), and then simplifying.

✦ We obtain \(r(x) = 24 + 19x + 16x^2 + 24x^3 − 26 − 25x − 22x^2\)
= \(39 + 35x + 35x^2 + 24x^3\)

✦ So, \(f(x) × g(x) = r(x) = 39 + 35x + 35x^2 + 24x^3\) in \(R_q\).

Representing polynomials as vectors

✦ A polynomial \(f(x) = a_0 + a_1x + ⋯ + a_{n−1}x^{n−1}\) in \(R_q = ℤ_q[x]/(x^n + 1)\) can be represented by its vector of coefficients \(f = (a_0, a_1, …, a_{n−1})\) The vector has length exactly \(n\) .

✦ Example: Consider \(R_q = ℤ_{41}[x]/(x^4 + 1) .\)

✦ The polynomials \(f(x) = 23 + 11x^2 + 7x^3 ∈ Rq\) and \(g(x) = 40 + 5x + 16x^2 ∈ R_q\) can be represented by the vectors \(f = (23, 0, 11, 7)\) and \(g = (40, 5, 16, 0)\) .
✦ In \(R_q\) , we have f+g = (22,5,27,7), f − g = (24, 36, 36, 7), and f × g = (12, 3, 29, 7)

« 回到首页