Table of contents
NIST 标准
KEM 介绍
ML-KEM 原理
域参数 和 密钥生成
对于ML-KEM-768:
q = 3329
n = 256
k = 3
η1 = 2
η2 = 2
密钥生成:
- 公钥 (A,t), 其中 \(A \in R_q^{k×k}\), \(s \in S_{η1}^k\),\(e \in S_{η2}^k\) , \(t = As + e\),用于加密.
- A是均匀随机生成的kxk矩阵,
- s是k维的小多项式向量,系数大小最多为η1;
- e是k维的小多项式向量,系数大小最多为η2;
- 私钥 \(s \in S_{η1}^k\) ,用于解密
加密
加密 一个\(m\in\{0,1\}^n\)
- Bob 获取 公钥 (A,t)
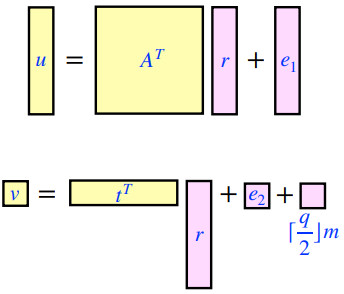
- 选择 \(r \in _RS^k_{η_{1'}} , e_1 \in _RS^k_{η_{2'}} 且\ e_2 \in _RS^k_{η_{2'}}\). η1’为η1 ,η2’ 为η2
- 计算密文(u,v)
\(u = A^Tr + e_1 , \\ v = t^Tr + e_2 + \lceil q/2 \rceil m\)
解密
Alice可以使用私钥s解密 \(m = Round_q(v - s^Tu) \\ =Round_q(t^Tr + e_2 + \lceil q/2 \rceil m - s^Tu) \\ =Round_q(t^Tr + e_2 + \lceil q/2 \rceil m - (s^TA^Tr+s^Te_1)) \\ =Round_q((As+e)^Tr + e_2 + \lceil q/2 \rceil m - (s^TA^Tr+s^Te_1)) \\ =Round_q(s^TA^Tr + e^Tr + e_2+ \lceil q/2 \rceil m - (s^TA^Tr+s^Te_1))\\ =Round_q(\lceil q/2 \rceil m+ e^Tr + e_2 - s^Te_1)\)
其中 \(size(e^Tr) = nη_2η_{1'} = 256*2*2 = 1024\),
其中 \(size(s^Te_1) = nη_1η_{2'} = 256*2*2 = 1024\)
Toy example - Kyber PKE (参数设置小只是为了方便展示)
Domain parameters:
✦ Key generation: Alice selects:
\(q =137\\ n=4\\ k=2\\ η_1=2\\ η_2=2\)
\(A = \begin{bmatrix} 21 + 57x + 78x^{2}+43x^{3}&126 + 122x + 19x^{2}+125x^{3}\\ 111 + 9x + 63x^{2}+33x^{3}&105 + 61x + 71x^{2}+64x^{3} \end{bmatrix}\) \(s = \begin{bmatrix} 1 + 2x - x^{2}+2x^{3} \\ -x + 2x^{3} \end{bmatrix}, \quad \\ e = \begin{bmatrix} 1 - x^{2}+x^{3} \\ -x + x^{2} \end{bmatrix}\) 并且计算 \(\\ t = As + e = \begin{bmatrix} 55 + 96x + 123x^{2}+ 7x^{3}\\ 32 + 27x + 127x^{2}+ 100x^{3} \end{bmatrix}\) 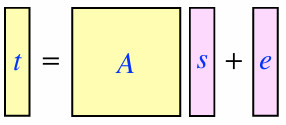
Alice的公钥(A,t)用于加密,私钥s用于解密
toy example: 加密
Bob进行加密: 首先,消息编码为 多项式: \(m=0111 ↔ x+x^2+x^3\) ,接着Bob选择 \(r, e_1, e_2\)
其中 \(r = \begin{bmatrix}-2 + 2x + x^{2}-x^{3}\\-1 + x + x^{2}\end{bmatrix}, \quad e_1 = \begin{bmatrix}1 - 2x^{2}+x^{3}\\-1 + 2x - 2x^{2}+x^{3}\end{bmatrix}, \quad e_2 = 2 + 2x - x^{2}+x^{3}\)
然后计算: \(u = A^Tr + e_1=\begin{bmatrix}56 + 32x+77x^2 + 9x^3\\45 + 21x+2x^2+127x^3\end{bmatrix} \\ \\ v = t^Tr + e_2+ 69m = 3 + 10x + 8x^2 + 123x^3\) 密文 c = (u,v)
toy example: 解密
Alice使用她的解密密钥s,计算 \(v - s^Tu = 4 + 60x + 79x^2 + 66x^3\) 且,round之后,q/4 = 137/4=34.25,即 [-34,34] 的系数设置为0,其余[35,68]∪[-68,-35] 为1: 得到round之后的多项式 \(0 + 1x^1 + 1x^2 + 1x^3\) 于是 恢复了原消息:0111
Rounded value ◄─────────────┐ ┌────────────►
└─────────────────────────┘
Modsq value ──────────────┬────────────┬────────────┬─────────────
-q/2 -q/4 0 +q/4 q/2
Raw value ──────────────────────────────────────────────────────
0 q
安全性
声称:假设 D-MLWE 问题难以解决,简化的 Kyber-PKE 方案在选择明文攻击(chosen-plaintext attack)下具有不可区分性。
论据: 加密操作: \(\begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} A^T \\ t^T \end{bmatrix} r + \begin{bmatrix} e_1 \\ e_2 \end{bmatrix} + \begin{bmatrix} 0 \\ \left\lceil \frac{q}{2} \right\rfloor \end{bmatrix} m\)
根据 D-MLWE 假设,\(\begin{bmatrix} A^T \\ t^T \end{bmatrix}\) 与随机数无法区分。 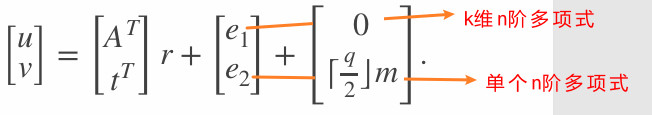
同样根据D-MLWE 假设, \(\begin{bmatrix} A^T \\ t^T \end{bmatrix}r + \begin{bmatrix} e_1 \\ e_2 \end{bmatrix}= \begin{bmatrix} A^Tr + e_1 \\ t^Tr + e_2 \end{bmatrix}\) 与随机数无法区分。
因此,从对手的角度来看,\(v\) 似乎是 \(R_q\) 中随机元素 \((\boldsymbol{t}^T\boldsymbol{r} + e_2)\) 与消息多项式 \(\left\lceil\frac{q}{2}\right\rceil m\) ,所以对手无法得知关于 (m) 的任何信息。
解密并不总是有效
问题:解密是否有效?即, \(m = \mathrm{Round}_q (v - s^T u)\)是否成立?
首先之前讨论过 \((v - s^Tu) \\ =(\lceil q/2 \rceil m+ e^Tr + e_2 - s^Te_1)\)
那么我们让 \(u' = u + e_u, \\ v' = v + e_v\) 则 \((v' - s^Tu') \\ =\lceil q/2 \rceil m+ e^Tr + e_2 - s^Te_1 + e_v - s^T e_u\)
因此,如果误差多项式\(E(x)=e^Tr + e_2 - s^Te_1+ e_v - s^T e_u\)的每个系数$E_i$满足 \(-q/4 < E_i \bmod q < q/4\),即\(\|E\|_{\infty}<q/4\),则\(\text{Round}_q(v - s^Tu)=m\)。
现在,\(\|E_i\|_{\infty}\leq kn\eta_1\eta_2+\eta_2+kn\eta_1\eta_2\)。
对于ML - KEM - 768参数(\(q = 3329, n = 256, k = 3, \eta_1=\eta_2 = 2\)),我们有 $|E_i|_{\infty}\leq6146 \nless q/4$。因此,不能保证解密成功。
然而,可以证明以接近1的概率$|E|_{\infty}<q/4$。因此,解密几乎肯定会成功。
V2b:优化
密钥的字节大小以及密文的字节大小
为了具体起见,我们将考虑ML-KEM-768 parameters(\(q = 3329, n = 256, k = 3, \eta_1 = 2, \eta_2 = 2\))。 在\(\mathbb{Z}_q\)中,整数的位长度是\(\lceil \log_2 3329 \rceil = 12\)位。
加密密钥:加密密钥\((A, t)\)的字节大小是 \((3^2 \times 256 \times 12)+(3 \times 256 \times 12) = 36864\text{位}\),即4608字节。
密文:密文$c = (u, v)$的字节大小是 \((3 \times 256 \times 12)+(256 \times 12) = 12288 \text{位}\),即1536字节。
更小的密钥
想法:从随机(且公开)的256位种子\(\rho\)生成A。
通过首先选择\(\rho \in_R \{0, 1\}^{256}\),然后通过对计数器哈希\(\rho\)来生成多项式的系数,从而生成A中的多项式。
加密密钥是\((\rho, t)\)而不是\((A, t)\)。
任何知道\(\rho\)的人都可以生成A。
现在加密密钥的大小是\(256 + (3 \times 256 \times 12)\)位,即1184字节(相比4608字节大幅减少)。
Compress
想法: 丢弃密文\(c = (u, v)\)中所有多项式系数的“低阶”位。
设\(1 \leq d \leq \lfloor \log_2 q \rfloor\),并定义: 对于\(x \in [0, q - 1]\),\(Compress_q(x, d)=\lceil (2^d/q) \cdot x \rceil \bmod 2^d\)。 对于\(y \in [0, 2^d - 1]\),\(Decompress_q(y, d)=\lceil (q/2^d) \cdot y \rceil \bmod q\)。
事实: 设$x \in [0, q - 1]$且$x’ = \text{Decompress}q(\text{Compress}_q(x, d), d)$。 那么$|x’ - x|{\infty} \leq \lfloor q/2^{d + 1} \rfloor$。
函数“压缩”和“解压缩”自然地扩展到$R_q$中的多项式以及$R_q^k$中的多项式向量。
中心二项式分布
快速多项式乘法
ML-KEM 计算工具
openssl 3.5.0 对于 ML-KEM 的应用
ML-KEM密钥对生成
openssl genpkey -algorithm ML-KEM-512 -out ML-KEM-512_priv.pem
ML-KEM密钥对打印
openssl pkey -in ML-KEM-512_priv.pem -noout -text
ML-KEM公钥导出
openssl pkey -in ML-KEM-512_priv.pem -pubout -out ML-KEM-512_pub.pem
公钥打印
openssl pkey -pubin -in ML-KEM-512_pub.pem -noout -text